L'Oligopole

Un duopole est une industrie composée de 2 firmes.

Un oligopole est une industrie composée de très peu de firmes.

L’impact : les décisions d’une firme se répercutent sur les profits de l’autre.

Chaque firme prend donc en compte les décisions de l’autre firme quand elle établit sa stratégie.

=> Théorie des Jeux !

Nous allons analyser le cas simple de 2 firmes qui produisent un bien identique.

Compétition par les quantités

L'hypothèse de base est que les firmes se font concurrence en fixant les quantités produites.

Si la firme 1 produit Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle y_1} unités et la firme 2 produit $y_{2}$ unités, alors la quantité offerte totale est $y_{1}+y_{2}$. Le prix de marché est $p(y_{1}+y_{2})$.

Les fonctions de coûts : $c_{1}(y_{1})$ et $c_{2}(y_{2})$.

Si la firme 1 prend la production de la firme 2 comme donnée, sa fonction de profit s’écrit $\pi _{1}(y_{1};y_{2})=p(y_{1}+y_{2})y_{1}-c_{1}(y_{1})$.

Etant donné $y_{2}$, quelle production $y_{1}$ maximise les profits de la firme 1 ?

Exemple : demande est $p(y_{T})=60-y_{T}$ et les fonctions de coûts sont $c_{1}(y_{1})=y_{1}^{2}$ et $c_{2}(y_{2})=15y_{2}+y_{2}^{2}$

La fonction de profit de la firme 1 :

$\Pi (y_{1};y_{2})=(60-y_{1}-y_{2})y_{1}-y_{2}^{1}$

Le choix optimal de la firme 1 :

${\frac {\partial \Pi }{\partial y_{1}}}=60-2y_{1}-y_{2}-2y_{1}=0$

I.e. La meilleure réponse de la firme 1 à la quantité produite par 2 est :

$y_{1}=R_{1}(y_{2})=15-{\frac {1}{4}}y_{2}$

La “courbe de réaction”.

La fonction de profit de la firme 2 :

$\Pi (y_{2};y_{2})=(60-y_{1}-y_{2})y_{2}-15y_{2}-y_{2}^{2}$

...le choix optimal de la firme 2...

${\frac {\partial \Pi }{\partial y_{2}}}=60-y_{1}-2y_{2}-15-2y_{2}=0$

I.e. La meilleure réponse de la firme 2 :

$y_{2}=R_{2}(y_{1})={\frac {45-y_{1}}{4}}$

La courbe de réaction de la firme 2.

Un équilibre de Nash ici, signifie que chaque firme joue sa meilleure réponse à la meilleure réponse de l’autre.

Une paire ($y_{1}^{*},y_{2}^{*}$) est un équilibre Cournot-Nash si $y_{1}^{*}=R_{1}(y_{2}^{*})$ et $y_{2}^{*}=R_{2}(y_{1}^{*})$.

La courbe de réaction de la firme 2.

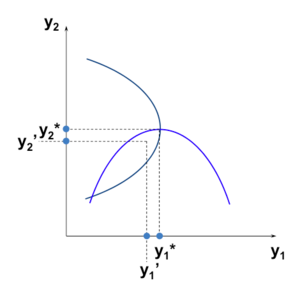
Courbes d’Iso Profit

Pour la firme 1, une courbe d’iso profit contient toutes les paires ($y_{1},y_{2}$) qui donnent à la firme 1 le même niveau de profit $\pi _{1}$.

Va nous permettre d’analyser les comportements collusifs.

Avec $y_{1}$ fixé, le profit de la firme 1 augmente quand $y_{2}$ diminue.

Si Firme 2 choisit $y_{2}=y_{2}^{'}$, quel est le niveau de production qui maximise le profit de 1 ?

A: Le point qui atteint la courbe la plus basse sur le graphe.

C’est la meilleure réponse de la firme 1 à $y_{2}^{'}$

La courbe de réaction de la firme 1 passe par les “sommets” des courbes d’iso-profit.

Collusion

Est-ce que les profits à l’équilibre de Cournot-Nash sont les plus élevés que les firmes peuvent atteindre au total ?

($y_{1}^{*},y_{2}^{*}$) : équilibre de Cournot.

($y_{1}^{'},y_{2}^{'}$) apporte de plus hauts profits à chaque firme que ($y_{1}^{*},y_{2}^{*}$).

Il y a donc des incitations pour les firmes à “coopérer” en diminuant leurs quantités produites: la collusion. Les firmes forment alors un cartel.

Analyse de ces cartels.

Coopération: l’objectif est de maximiser les profits joints, et ensuite de les partager.

Objectif : trouver les quantités qui maximisent

$\Pi ^{m}(y_{1},y_{2})=p(y_{1}+y_{2})(y_{1}+y_{2})-c_{1}(y_{1})-c_{2}(y_{2})$

Condition sur le partage : aucune firme ne doit avoir moins que les profits qu’elle obtiendrait à l’équilibre de Cournot-Nash.

($y_{1}'',y_{2}''$) offre le maximum de profit joint.

$({\tilde {y}}_{1},{\tilde {y}}_{2}$ donne les profits maximum à la firme 1 et le niveau de profit de l’équilibre Cournot Nash à la firme 2.

($y_{1}^{m},y_{2}^{m}$) maximise le profit joint.

Un tel cartel est-il stable ?

I.e. si la firme 1 produit $y_{1}^{m}$ unités, est-ce que la firme 2 ne peut pas faire mieux que produire $y_{2}^{m}$ unités ?

Meilleure réponse de la firme 2 à $y_{1}=y_{1}^{m}$ est $y_{2}=R_{2}(y_{1}^{m})$.

$y_{2}=R_{2}(y_{1}^{m})$ est la meilleure réponse de 2 à $y_{1}=y_{1}^{m}$.

Meilleure réponse : $y_{2}=R_{2}(y_{1}^{m})>y_{2}^{m}$.

La firme 2 augmente ses profits en déviant du cartel, en produisant $R_{2}(y_{1}^{m})$.

De même la firme 1 peut augmenter ses profits en déviant de $y_{1}^{m}$ à $R_{1}(y_{2}^{m})$.

Un cartel, composé de firmes qui recherchent leur profit individuel, est fondamentalement instable.

En pratique, comment un cartel peut-il se maintenir ? Exemple ?

Meneur et suiveur...

Jusqu’à présent, l'hypothèse est que les firmes jouaient simultanément. Nous allons désormais analyser un jeu séquentiel.

La firme 1 choisit ses quantités en 1er et la firme 2 suit: firme 1 est le “meneur” et la firme 2 est le “suiveur”. Le jeu devient ainsi un jeu séquentiel, avec les quantités produites comme variable stratégique.

Ces jeux s’intitule des jeux de Stackelberg.

Vaut-il mieux être le meneur ou le suiveur ?

Jeu de Stackelberg

Quel est le meilleur choix de la firme 2 quand elle observe le choix de la firme 1 ?

=> $y_{2}=R_{2}(y_{1}).$

La firme 1 connait cette meilleure réponse, et l’anticipe donc quand elle choisit sa quantité.

“Induction à rebours” : équilibre en sous-jeu.

La fonction de profit du meneur :

$\Pi _{1}^{m}(y_{1})=p(y_{1}+R_{2}(y_{1}))y_{1}-c_{1}(y_{1})$

Le meneur choisit $y_{1}$ pour max. ses profits.

Il va faire des profits plus important qu’à l’éq. De C-N, pourquoi ?

($y_{1}^{*},y_{2}^{*})$ : éq. de Cournot-Nash.

Courbe de réaction du suiveur.

($y_{1}^{S},y_{2}^{S}$): éq. de Stackelberg.

Que se passe-t-il si les firmes font une concurrence par les prix et non par les quantités ? => Jeux de Bertrand.

Jeu de Bertrand

Chaque firme a un coût marginal constant: c.

Toutes les firmes fixent leur prix simultanément.

Existe-t-il un équilibre de Nash ?

Oui, un seul équilibre: toutes les firmes annoncent un prix exactement égal à c (comme en concurrence parfaite).

Raisonnement : si la firme 1 annonce un prix élevé (i.e. prix de monopole) quelle est la meilleure réponse de 2 ?

Quelle est la meilleure réponse de 1 à cette stratégie ?

Jeu de prix séquentiel

Ici une firme fixe un prix en premier (meneur) et d’autres firmes suivent en fixant un prix ensuite (suiveurs).

On peut penser à une large firme (meneur) et beaucoup de petites firmes suiveuses. Les petites firmes sont preneuses de prix, et leur fonction d’offre agrégée est Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Y_s(p)} .

La fonction de la demande est comme suit : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle D(p)} .

Le meneur sait donc que s’il fixe un prix Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p} , il fera face à la demande résiduelle : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle L( p) = D( p) - Y_S(p)}

Sa fonction de profit est donc  : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \Pi_m(p) = p(D(p) - Y_S(p)) -c_m (D(p) -Y_s(p))}

Le meneur choisit donc le Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p^*} qui maximise ce profit. Et les suiveurs fournissent Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Y_s(p^*)} unités. Le meneur fournit la demande résiduelle Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle D(p^*) - Y_s(p^*)} .